ベイズ的検定：あり得ないモデル（演習12.2）

「『確かめる』ことは『違いの有無を見つける』こと」からの続き。


Exercise 12.2 の演習とその解法を Solutions to Exercises in Doing Bayesian Data Analysis Second Edition から引用する。日本語訳は要約と意訳、それに若干の補足を加えたもの。なお、(A), (B) は前回の投稿と同じ実験。


[Purpose: Model comparison for different partitions of group modes, using the script of Section 12.2.2.1.]

Open the script OneOddGroupModelComp2E.R, making sure that R's working directory includes the various utility programs used with this book.

(A) For this part of the exercise, the goal is to reproduce the findings presented in Section 12.2.2.1. First, be sure that the prior probabilities on the models are set to 50/50:

modelProb[1] <- 0.5
modelProb[2] <- 0.5

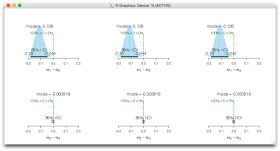
Run the script and report the results, including the graphs for the model index and the modes and differences of modes. State what the two models are, and state which model is preferred and by how much. (Hint: Model 2 is the single-mode, and it is preferred.)

The shape parameters of the beta distribution are determined by the model index, as this code snippet shows:

# Use omega[j] for model index 1, omega0 for model index 2:
aBeta[j] <-      (equals(mdlIdx,1)*omega[j] 
                      + equals(mdlIdx,2)*omega0)  * (kappa[j]-2)+1
bBeta[j] <- (1 - (equals(mdlIdx,1)*omega[j] 
                      + equals(mdlIdx,2)*omega0)) * (kappa[j]-2)+1

When mdlIdx is 1, then omega[j] is used, and when mdlIdx is 2, then omega0 is used.

The plots of the model index, above, indicate that the ESS of model-index chain is about 3,000, which is not too bad for our purposes. Model index 2 is preferred, with a posterior probability of about 85%. In other words, the single-mode model is preferred to the four-mode model.

model-index 連鎖の ESS が約 3,000 は、今回の目的からすれば悪くない。約 87 %の割合で、モデル 2 の方が好まれた。つまり「モードが 1 つのモデル」が「モード 4 つのモデル」より好まれた。


(B) Continuing with the previous part, consider the graphs of differences of modes. What do they imply about differences between groups? Does this conclusion agree or disagree with the conclusion from the model comparison? How do you reconcile the conclusion? (Hint: The model index and the groups modes are all parameters being simultaneously estimated, so there is no contradiction. The parameters answer different questions; which questions?)

この結果から、モードの違いを考える。グループ間の違いは？この結論は、モデル比較の結論と矛盾しないか？（ヒント：モデル index とグループ modes は同時に推定されるパラメータのため、矛盾はない。パラメータが答えてるのは別の質問、どの質問か？）

Despite the single-mode model being preferred, some differences of modes (e.g., ω₁ - ω₄) appear to be noticeably different, as shown by the posterior distribution of the difference, above. This seems to disagree with the conclusion from the model comparison. But there is no real contradiction because the model index and the group modes are being simultaneously estimated. The group modes are close enough together that the single-mode model can account for the data better than the four-mode model when taking into account the prior being diluted over a larger parameter space. The posterior on the model-index addresses the question of which prior better accounts for the data; the posterior on the four mode parameters addresses the question of what are credible estimates of the group modes.

モデル比較では「モードが 1 つのモデル」が好まれた。しかし、例えば ω₁ - ω₄ のように、モードの差が明らかなものがある。これは、モデル比較の結論と矛盾する。（つまり、モードが 1 つということは「グループ間で違いがない」を前提としたモデルだから）。モデル選択が答えるのは、適切な事前確率はどれかという質問。4 つのモードのパラメータの事後確率が答えるのは、グループモード推定の確からしさへの質問。


(C) For this part of the exercise, the goal is to compare the single-mode model against a different partitioning of the group modes. Instead of letting each group have its own distinct mode, we will allow a distinct mode for the first group. but restrict groups 2 through 4 to use a single mode. One way to accomplish this is to change this part of the model specification:

   for ( j in 1:nCond ) {
     # Use omega[j] for model index 1, omega0 for model index 2:
     aBeta[j] <-       ( equals(mdlIdx,1)*omega[j] 
                       + equals(mdlIdx,2)*omega0  )   * (kappa[j]-2)+1
     bBeta[j] <- ( 1 - ( equals(mdlIdx,1)*omega[j] 
                       + equals(mdlIdx,2)*omega0  ) ) * (kappa[j]-2)+1
   }
   for ( j in 1:2 ) {
     omega[j] ~ dbeta( a[j,mdlIdx] , b[j,mdlIdx] )
   }
   omega[3] <- omega[2]
   omega[4] <- omega[2]

#  for ( j in 1:nCond ) {
#    # Use omega[j] for model index 1, omega0 for model index 2:
#    aBeta[j] <-       ( equals(mdlIdx,1)*omega[j] 
#                      + equals(mdlIdx,2)*omega0  )   * (kappa[j]-2)+1
#    bBeta[j] <- ( 1 - ( equals(mdlIdx,1)*omega[j] 
#                      + equals(mdlIdx,2)*omega0  ) ) * (kappa[j]-2)+1
#    omega[j] ~ dbeta( a[j,mdlIdx] , b[j,mdlIdx] )
#  }

グループの個々にモードがあるのではなく、グループ 1 と他の 3 グループでモードが異なる。つまり、グループ 2, 3, 4 は同じ「モードが 2 つのモデル」を考える。

In your report, carefully explain what the change does. Make the change, and run the script (with the prior probabilities on the models set to 50/50). Report the results, including the graphs for the model index and the modes and differences of modes. State what the two models are, and state which model is preferred and by how much. (Hint: Model 2 is the ingle-mode model, and it is not preferred.)


次が実行結果。

We see above that model index 1 (the two-mode model) is strongly preferred, with a posterior probability of about 94%. Thus, although the single-mode model is preferred to the four-mode model, this particular two-mode model is preferred to the single-mode model.

「モードが 1 つのモデル」の方が、「4 つのモードのモデルより好ましい」かったが、「2 つのモードのモデル」の方が「1 つのモードモデル」より好ましい。


(D) Continuing with the previous part, consider the graphs of differences of modes. What do they imply about differences between groups? Does this conclusion agree or disagree with the conclusion from the model comparison? Even though Model 1 is preferred, is it really meaningful?

「2 つのモードのモデル」が好まれたが、これは意味のある結果か？

The posterior distribution on ω₁ - ω₂ shows that estimated magnitude of difference clearly excludes zero. But since ω₂ = ω₃ = ω₄, the differences of the latter three group modes are exactly zero. Is this really meaningful? Even though this model is preferred to the single-mode model, do we really think that ω₂ = ω₃ = ω₄ exactly? This seems like an implausible model in the first place, and it should have a small prior probability. One the other hand, so should the single-mode model. It seems we are comparing one implausible model against another implausible model.

ω₂ = ω₃ = ω₄ なのか？この三つの条件のモードが完全に一致している、という前提自体がそもそもあり得ない。したがって、そんなモデルも非現実的。したがって、全ての条件でモードが同じとする「モードが 1 つのモデル」との比較は、あり得ないモデルと別のあり得ないモデルを比較しているにすぎない。


(E) Considering the results of the previous parts, what seems to be the most meaningful approach to analyzing differences of groups? (I'm hoping you'll say parameter estimation, not model comparison. But you might give arguments to the contrary.) Can you think of other applications in which model comparison might be more useful?

これまでの結果から、グループの違いを分析する最も意義のある方法はどれか？（モデル比較ではなく、パラメータ推定と答えてくれることを望む。）では、モデル比較が有用な場合は？

If it is not plausible that the group modes are truly and exactly identical, then the most meaningful approach is to estimate their magnitudes and make decisions based on the posterior distribution of the modes. N.B.: Model comparison can be useful when both models are plausible and equivalently informed by previous data.

グループモードが一致するのが不自然ならば、最も意味のある方法は、モード値の事後確率分布をもとにして決めること。注意：モデル比較が有用になり得るのは、両モデルがもっともらしく、観測データが加味されている場合。